Independent Chip Model (ICM)
Das Independent Chip Model (ICM) ist ein Konzept, welches jeder Pokerspieler kennen muss, der langfristig profitabel Turniere (vor allem Sit & Go) spielen möchte. Spieler, die dieses Konzept nicht kennen, treffen während des ganzen Turniers Entscheidungen, die nicht profitabel oder bei weitem weniger profitabel sind als vermutet. Dies gilt insbesondere für die Phase kurz vor Erreichen des Preisgelds (Bubble Play), wo man immer wieder erschreckend falsche Entscheidungen sieht. Man darf fast schon von Dummheiten sprechen!
Das ICM ist ein Modell, mit dessen Hilfe anhand der Stack Grössen der im Turnier verbleibenden Spieler die jeweilige Wahrscheinlichkeit berechnet wird, dass ein Spieler Erster, Zweiter oder Dritter wird.
Wofür kann man das ICM verwenden?
- Deine zwei verbleibenden Gegner eines sehr grossen Turniers offerieren dir einen Deal und du möchtest nachrechnen, ob du einen fairen Preis bekommst. Mehr dazu in separatem Artikel: Berechnung von Deals am Final Table eines Pokerturniers.
- Du möchtest entscheiden, ob du ein All-In eines Gegenspielers in einer späten Phase des Turniers (oder vor dem Bubble) callen willst.
Die mathematischen Grundlagen
Im Modell geht man davon aus, dass die Chance, ein Turnier zu gewinnen so hoch ist, wie die Anzahl eigener Chips im Verhältnis zu allen im Turnier vorhandenen Chips.
Beispiel:
Vier Spieler verbleiben in einem Sit & Go, bei dem zehn Spieler mit jeweils 1’000 Chips begonnen haben. Spieler A hat 5’000 Chips, Spieler B hat 3’000 Chips, Spieler C hat 1’500 Chips und Spieler D hat noch 500 Chips.
Gemäss dem ICM sind somit die Wahrscheinlichkeiten eines Turniersiegs wie folgt:
- Spieler A: 50 % (5’000 Chips dividiert durch die Total sich im Umlauf befindenden 10’000 Chips)
- Spieler B: 30 % (3’000 Chips dividiert durch 10’000 Chips)
- Spieler C: 15 % (1’500 / 10’000 )
- Spieler D: 5 % (500 / 10’000)
Anhand des ICMs kann nun auch die Wahrscheinlichkeit jedes einzelnen Spielers errechnet werden, Rang 2, Rang 3 usw. zu erreichen. Stellt man nun diese Wahrscheinlichkeiten dem möglichen Gewinn gegenüber, so erhält man den «erwarteten Wert» (Englisch: Expected Value, oft auch Equity genannt) bei der aktuellen Turniersituation.
Um diesen erwarteten Gewinn zu berechnen, gibt es diverse Internet Poker Tools. Wir können für Sit & Gos folgenden ICM Rechner empfehlen: Kurzbeschreibung ICM Rechner.
Wichtig zu wissen ist auch, dass das ICM nur den erwarteten Gewinn anhand der Chips berechnet. Die Fähigkeiten der Spieler, oder die aktuelle Position der Blinds werden dabei nicht berücksichtigt. Bei sehr hohen Blinds hat die Position des Buttons (und wer als nächstes die Blinds bezahlen muss) einen erheblichen Einfluss.
Erwarteter Wert anhand des obigen Beispiels
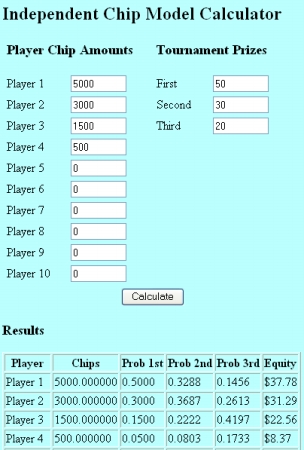
Weitere Annahme: Es handelt sich um ein 10 + 1 $ Buy-In Turnier. Der erste Rang erhält 50$ ausbezahlt, der zweite Rang 30$ und der dritte Rang 20$.
Ganz ehrlich, Spieler D, der nur noch 500 Chips hat, müsste doch einen erwarteten Wert haben, der zehn Mal niedriger ist, als derjenige von Spieler A mit 5’000 Chips? Eben nicht! In nebenstehender Abbildung sehen wir das Resultat, welches belegt, dass jeder zusätzlich gewonnene Chip weniger Wert hat als die zuvor gewonnenen Chips.
Kurze Erklärung zu den Spalten:
- Prob 1st = Wahrscheinlichkeit Erster zu werden
- Prob 2nd = Wahrscheinlichkeit Zweiter zu werden
- Prob 3rd = Wahrscheinlichkeit Dritter zu werden
- Equity = Erwarteter Wert in der aktuellen Situation (Wahrscheinlichkeit Sieg multipliziert mit Auszahlung Rang 1, Wahrscheinlichkeit zweiter Rang multipliziert mit Preisgeld Rang 2 usw.)
Anmerkung: Nur wenn ein einziger Spieler einen Preis bekommt (Winner takes it all), hat jeder Chip linear den gleichen Wert.
Was fangen wir nun mit diesen Zahlen an?
Beispiel 1
Gehen wir davon aus, du bist in unserem Beispiel Spieler B mit 3’000 Chips. Die Blinds sind 100/200. Du hast soeben als BB 200 Chips abgegeben. Auf dem Small Blind ist Spieler A. Spieler C und D folden, Spieler A (mit 5’000 Chips) geht All-In. Du hast JJ. Spieler A war bisher solide und ist nie mit komplettem ‹Müll› All-In gegangen. Nun können wir mit dem ICM Folgendes berechnen: vor der Hand ist dein erwarteter Gewinn 31.29$. Es gibt nun drei mögliche Varianten (die Möglichkeit eines Split-Pots bei einem Call lassen wir mal ausser Betracht):
- 1. Variante: Du foldest. Nach dieser Hand hast du noch 2’800 Chips und Spieler A 5’200 Chips. Dein erwarteter Gewinn sinkt auf 30.52$. Du verlierst 0.77$ an erwartetem Gewinn.
- 2. Variante: Du callst und gewinnst. Du hast somit 6’000 Chips. Spieler A noch 2’000 Chips. Dein erwarteter Gewinn beträgt nun 40.59$. Du hast 9.30$ an erwartetem Gewinn dazu gewonnen.
- 3. Variante: Du callst und verlierst. Du bist draussen. Dein erwarteter und diesmal definitiver Gewinn ist 0. Du verlierst somit 31.29$ an erwartetem Gewinn.
Das Ergebnis ist ernüchternd! Du kannst sehr viel verlieren, aber kaum etwas dazu gewinnen! Auf welche Hand musst du den Gegner setzen, damit sich dieser Call trotzdem lohnt?
Mögliche Hände der Gegner und Auswirkungen:
- 1. Variante, dein Gegner hat zwei höhere Karten, also AK oder AQ.
In diesem Falle bist du gemäss Odds Calculator ca. 57% zu 43% Favorit, die kleine Möglichkeit eines Split Pots lassen wir der Einfachheit halber weg. Anmerkung: Wenn dir dein Gegner diese Hand in einem Cash Game zeigen würde, müsstest du unbedingt mitgehen! Bei einem Cash Game kommt es nicht auf die Auszahlungsstruktur an, da du im Falle einer Niederlage zum nächsten Bankomaten gehen und dir auf dem Weg überlegen kannst, wie grausam Poker manchmal sein kann (im Wissen, dass du das Richtige gemacht hast).. Wir rechnen: In 43% der Fälle verlierst du und dein erwarteter Gewinn ist 0. In 57% der Fälle ist dein erwarteter Gewinn 40.59 $. Das heisst, bei einem Call ist dein erwarteter Gewinn 40.59 $ * 57/100 (57 %), welches 23.13 $ ergibt. Somit ist ein Call nicht profitabel, bei einem Fold ist dein erwarteter Gewinn 30.52 $, ein Call senkt den erwarteten Gewinn auf 23.13 $. Statistisch gesehen verspielst du mit diesem einen Call 7.39 $, wenn dein Gegner einer dieser Kombinationen hält, obwohl du das bessere Startblatt hast! Langsam sollte es dämmern, warum es wichtig ist, als Chip Leader beim Bubble auf den mittelgrossen Stacks herumzuhacken! 😉 - 2. Variante, dein Gegner hat ein höheres Pärchen, also QQ, KK oder AA
Wir müssten hier nicht grossartig rechnen, du bist 1 zu 4 Underdog und ein Call wäre ganz schlecht. Wir rechnen aber trotzdem. Für das Beispiel nehmen wir an, dein Gegenspieler habe KK. (QQ wäre unangenehmer, da deine Straight Chancen sinken, AA wäre für dich etwas besser. KK ist die ‹goldene› Mitte). KK gewinnt in ca. 81% der Fälle gegen JJ. In 81% der Fälle ist dein erwarteter Gewinn = 0. In 19% der Fälle ist er 40.59 $. Ein Call gibt somit einen erwarteten Gewinn von 7.71 $. Ein Fold ergäbe wie schon erwähnt 30.52$, somit wird dein erwarteter Gewinn um 22.81$ reduziert. - 3. Variante, dein Gegner hat ein niedrigeres Pärchen.
Nehmen wir als Beispiel 99, denn mit einem noch tieferen Pärchen s(88 und tiefer) würde dein Gegner vermutlich nicht All-In gehen. Diesmal bist du 81 zu 19% Favorit. In 19% der Fälle sinkt dein erwarteter Gewinn auf 0. In 81% der Fälle steigt er auf 40.59$. Somit würde ein Call hier deinen erwarteten Gewinn auf 32.88$ (40.59*81/100) bringen. Wenn Du foldest, ist dein erwarteter Gewinn wie schon erwähnt 30.52$. In diesem Falle würde dir ein Call 2.36$ zusätzlichen erwarteten Gewinn bringen. Wow, nur 2.36$ Profit, obwohl du ein höheres gegen ein niedrigeres Pärchen spielst!!!
Schlussfolgerung von Beispiel 1
Wenn du am Bubble eines «konventionellen» Sit & Go Turniers spielst und eine komfortable Führung vor dem letzten (und/oder vorletzten) Gegenspieler hast, brauchst du ein super Startblatt (AA oder KK), um profitabel ein All-In des Chip Leaders callen zu können! Umgekehrt kannst du als Chip Leader sehr viel Druck auf deine Gegner ausüben! Vorsichtiges Spiel lohnt sich hier. Du foldest. In der Hand direkt darauf, wird Spieler D mit 500 Chips vom Chip Leader vom Tisch genommen (du musstest 100 Chips SB bezahlen). Jetzt sieht die Chip Verteilung so aus. Spieler A: 5’800 Chips. Spieler B (du): 2’700 Chips, Spieler C: 1’500 Chips. Gemäss ICM ist dein erwarteter Gewinn nun bei 33.20$. Obwohl du 300 Chips weniger hast, als vor zwei Händen, ist durch das Ausscheiden eines anderen Spielers dein erwarteter Gewinn um 2.68 $ gestiegen!
Beispiel 2
Es sind zwischenzeitlich einige Hände gespielt worden. Spieler A hat nun 5’500 Chips, Spieler B (du) hast 3’000 Chips und Spieler C hat 1’500 Chips. Die Blinds sind immer noch 100/200. Erneut bist du auf dem Big Blind. Spieler A auf dem SB geht All-In (er hat es in letzter Zeit etwas übertrieben, er kann unmöglich ständig so gute Startblätter haben, die diese Aggressivität rechtfertigen).
Deine Hand: wie schon oben, wieder JJ! Dies ist die selbe Situation wie oben, meinst du? Nicht ganz, denn im Falle eines Ausscheidens ist dein Gewinn nun 20.00 $ und nicht mehr 0 $. Wir rechnen nochmals durch. Wir haben nie behauptet, Poker habe nichts mit Mathematik zu tun!
Wenn du foldest, ist dein erwarteter Gewinn noch 32.61 $. Ein Minus von 0.59 $. Wenn du callst und verlierst, ist dein erwarteter Gewinn genau 20.00 $, nämlich das Preisgeld für Rang 3. Wenn du gewinnst, hast du 6’000 Chips und Spieler A noch 2’500 Chips. In diesem Falle ist dein erwarteter Gewinn 41.06 $.
Mögliche Hände der Gegner und Auswirkungen:
- 1. Variante, dein Gegner hat zwei höhere Karten, also AK oder AQ.
Wie oben erwähnt, du bist 57% zu 43% Favorit, den Split Pot lassen wir erneut bei Seite. Ausgangslage: In 43% der Fälle verlierst du und dein erwarteter Gewinn ist 20 $. Zu 57 Prozent gewinnst du und dein erwarteter Gewinn ist 41.06 $.
Wir rechnen: 41.06$ * 0.57 + 20.00 $ * 0.43 = 32.00 $
In diesem Falle würde ein Call deinen erwarteten Gewinn von 32.61$ (Vergleich immer im Bezug auf den erwarteten Gewinn, wenn man passt, also einen Fold macht) auf 32.00$ senken. Dein erwarteter Gewinn nimmt um 0.61 $ ab.
2. Variante, dein Gegner hat ein höheres Pärchen, also QQ, KK oder AA
Aus Beispiel eins wissen wir, dass du nur in 19 % der Fälle die Hand gewinnen wirst.
Wie bei Variante eins rechnen wir durch: 41.06$ * 0.19 + 20.00 $ *0.81 = 24.00 $.Dein erwarteter Gewinn würde somit um 8.61 $ sinken.
3. Variante, dein Gegner hat ein niedrigeres Pärchen.
Diesmal bist du 81 zu 19% Favorit.
Wir rechnen: 41.06$ * 0.81 + 20.00 $ * 0.19 = 37.06 $.
Somit hat dein erwarteter Gewinn um 4.45 $ zugenommen.
4. Variante, Spieler A spielt etwas in der Art von A8 oder A9.
Der Odds Calculator sagt uns, dass wir zu 72 % die Hand gewinnen.Wir rechnen wieder: 41.06 * 0.72 + 20.00 * 0.28 = 35.16$.
Dein erwarteter Gewinn würde bei einem Call in dieser Situation um 2.55 $ zunehmen.
5. Variante, Spieler A spielt tiefe Karten (geben wir ihm 87s, also Suited Connectors, wir nehmen an, kompletten ‹Müll› würde er nicht spielen).
Der Odds Calculator muss wieder ran und rechnet aus, dass wir zu 78 % die Hand gewinnen.Wir rechnen wieder: 41.06 * 0.78 + 20.00 * 0.22 = 36.43$.
Dein erwarteter Gewinn würde bei einem Call in dieser Situation um 3.82 $ zunehmen.
In Anbetracht der Umstände, solltest du in dieser Situation mitgehen, da in den meisten Fällen dein erwarteter Gewinn steigt.
Schlussfolgerung aus Beispiel 2
Auch wenn du bereits die Preisränge erreicht hast, lohnt es sich, das ICM Konzept zu kennen und anzuwenden! Gerade weil man den erwarteten Gewinn nicht im Kopf ausrechnen kann, ist es wichtig, dies bei verschiedenen Blind Levels durchzuspielen, damit man im Ernstfall wenigstens nicht die gröbsten Fehler macht! Viele Spieler wenden bei Sit & Go Turnieren auch vor dem Preisgeld konsequent das M-Konzept an! Das M-Konzept spielt sicher eine Rolle, dies alleine zu betrachten ist aber ein Fehler! Dein Return on Investment (ROI) wird stark zunehmen, wenn du dich mit ICM auskennst und dies befolgst! Das M-Konzept ist für die mittlere Mehrtisch-Turnierphase massgebend. Das ICM kommt vor allem bei Mehrtischturnieren mit steiler Preisstruktur und Sit & Gos zum Tragen! (Sit & Go Turniere haben im Vergleich zu den grossen Mehrtischturnieren eine extrem steile Preisstruktur!)
Bei unserer Sit & Go Strategie verweisen wir auf einen Artikel, bei dem ein Coinflip in früher Sit & Go Phase mit Einbezug des ICMs analysiert wird.
Eine kurze Anmerkung zum Schluss: In mehreren verschiedenen Poker Foren haben wir Aussagen gelesen, ICM sei nur bei einem höheren Buy-In (ab 20$ etc.) anwendbar. Dies ist absoluter Unsinn! ICM stellt eine mathematische Grundlage dar, die völlig unabhängig vom Buy-In funktioniert. Gerade bei den tiefen Buy-Ins kennen die wenigsten Spieler das ICM, was diese Turnierart für gute Spieler umso profitabler macht!
Deals berechnen
Mit Hilfe des Independent Chip Models lassen sich auch mathematisch exakte Deals in Pokerturnieren berechnen. Ein Beispiel dafür liefern wir dir im Artikel Deals bei einem Pokerturnier berechnen.
